Lista de questões Gravitação (capítulo 13)- Resolução das questões - Livro - Fundamentos de física, volume 2, 8ª edição, Halliday - Resnick
Livro - Fundamentos de f´ısica, volume 2, 8ª edi¸c˜ao, Halliday - Resnick
Cap´ıtulo - 13, problema 6: Na Figura, trˆes esferas de 5,00 kg est˜ao
localizadas a distˆancias d
1
= 0, 300m e d
2
= 0, 400m. (a) Qual ´e o m´odulo
e (b) qual a orienta¸c˜ao (em rela¸c˜ao ao semieixo x positivo) da for¸ca grav-
itacional total que as esferas A e C exercem sobre a esfera B?
Solu¸c˜ao:
Sabemos que a for¸ca gravitacional obedece o princip´ıo da superposi¸c˜ao.
Isto ´e, a for¸ca gravitacional resultante sobre B (
#”
F
B,res
) ser´a dada pela soma
vetorial entre a for¸ca gravitacional que A exerce sobre B (
#”
F
B,A
) e a for¸ca
gravitacional que C exerce sobre B (
#”
F
B,C
). Ent˜ao, escrevemos:
#”
F
B,res
=
#”
F
B,A
+
#”
F
B,C
(1)
De acordo com a figura do problema, podemos supor que a esfera B
est´a na origem de um plano cartesiano. Portanto, as for¸cas
#”
F
B,A
e
#”
F
B,C
est˜ao orientadas, respectivamente, no sentido positivo do eixo Y e X. Desta
maneira, podemos reescrever a equa¸c˜ao 1 da seguinte forma:
#”
F
B,res
= F
B,C
#”
i + F
B,A
#”
j (2)
Sendo assim, o m´odulo da for¸ca gravitacional total sobre B ´e:
|
#”
F
B,res
| =
q
F
2
B,C
+ F
2
B,A
1
|
#”
F
B,res
| =
s
G · m
C
· m
B
d
2
2
2
+
G · m
A
· m
B
d
2
1
2
Substituindo os valores do enunciado e sendo G = 6, 67 · 10
−11
m
3
kg·s
2
,
obtemos |
#”
F
B,res
| = 2, 13 · 10
−8
N.
Para a solu¸c˜ao do ´ıtem b, podemos utilizar as rela¸c˜oes trigonom´etricas no
triˆagulo retˆangulo formado pela for¸ca resultante e suas componetes para
determinar o ˆangulo θ que a
#”
F
B,res
faz em rela¸c˜ao ao eixo X positivo.
Vejamos:
tg(θ) =
|
#”
F
B,A
|
|
#”
F
B,C
|
(3)
tg(θ) =
G·m
A
·m
B
d
2
1
G·m
C
·m
B
d
2
2
=
G · m
A
· m
B
d
2
1
·
d
2
2
G · m
C
· m
B
=
d
2
2
d
2
1
Sendo m
A
= m
C
. Aplicando a fun¸c˜ao inversa da tangente em ambos
lados e substituindo os dados do enunciado, obtemos:
θ = tg
−1
d
2
2
d
2
1
= 60, 64
◦
Interpretando o resultado acima, ele est´a correto, pois a
#”
F
B,res
encontra-
se no primeiro quadrante do plano cartesiano.
■
2
Livro - Fundamentos de f´ısica, volume 2, 8ª edi¸c˜ao, Halliday -
Resnick
Cap´ıtulo - 13, problema 16: Na Figura, uma part´ıcula de massa m
1
= 0,67 kg est´a a uma distˆancia d = 23 cm de uma das extremidades de uma
barra homogˆenea de comprimento L = 3,0 m e massa M = 5,0 kg. Qual ´e
o m´odulo da for¸ca gravitacional que a barra exerce sobre a part´ıcula?
Solu¸c˜ao:
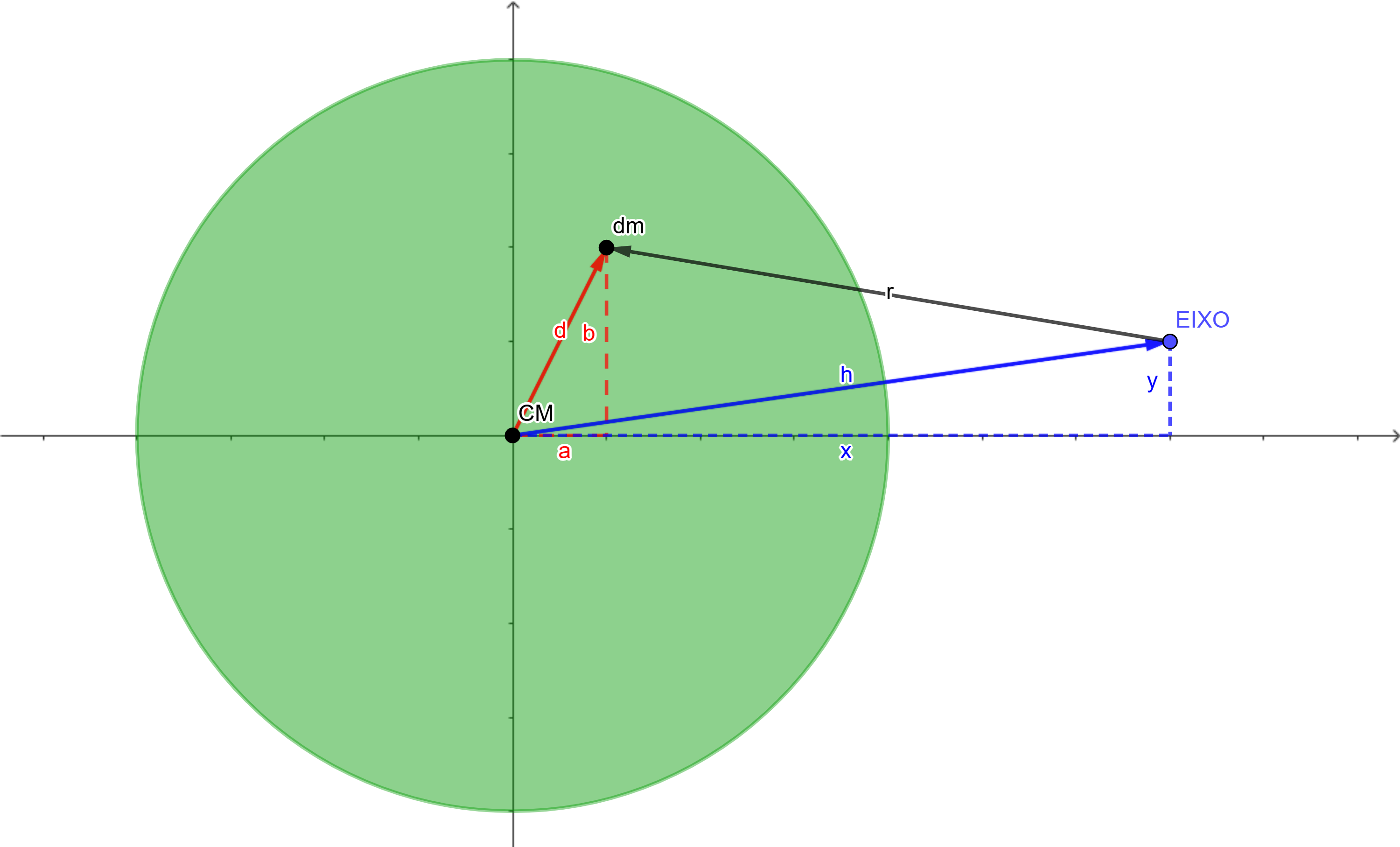
Nesta situa¸c˜ao podemos utilizar o princ´ıpio da superposi¸c˜ao para um
corpo extenso. Em outras palavras, cada elemento infinitesimal de massa
dm e comprimento dr da barra est´a exercendo uma for¸ca gravitacional
infinitesimal d
#”
F sobre a part´ıcula de massa m
1
. A equa¸c˜ao a seguir calcula
a for¸ca gravitacional exercida por um elemento infinitesimal da barra sobre
a part´ıcula.
d
#”
F =
G · m
1
· dm
r
2
#”
i (1)
´
E f´acil perceber, pela figura, que cada for¸ca infinitesimal d
#”
F est´a orien-
tada na dire¸c˜ao horizontal, no sentido da esquerda para a direita. Devido
a isso, expressamos a for¸ca d
#”
F em termos do vetor unit´ario
#”
i .
Portanto, ´e f´acil notar que devemos somar todas essas parcelas de for¸cas
exercidas sobre a part´ıcula para determinar a for¸ca gravitaciona resultante
#”
F
res
. No entanto, devido a quantidade extremamente grande de termos,
precisamos recorrer ao conceito de integral. Sendo assim, aplicamos a
integral em ambos os lados da equa¸c˜ao 1. Vejamos:
Z
d
#”
F =
Z
G · m
1
· dm
r
2
#”
i ⇒
#”
F
res
=
Z
G · m
1
· dm
r
2
#”
i (2)
3
Sendo
R
d
#”
F =
#”
F
res
. De acordo com o enunciado, a barra ´e homogˆenea.
Logo, a densidade linear ρ, que representa a quantidade de massa por
unidade de comprimento, ´e constante. Ou seja,
ρ =
M
L
=
dm
dr
⇒ dm =
M
L
dr (3)
Assim, podemos escrever a equa¸c˜ao 2 da seguinte forma:
#”
F
res
=
Z
G · m
1
· M
r
2
· L
dr
#”
i ⇒
#”
F
res
=
G · m
1
· M
L
Z
1
r
2
dr
#”
i (4)
Ent˜ao, o m´odulo da for¸ca resultante sobre a part´ıcula ´e dado por:
|
#”
F
res
| =
G · m
1
· M
L
Z
1
r
2
dr
#”
i
⇒ |
#”
F
res
| =
G · m
1
· M
L
Z
1
r
2
dr (5)
Definindo os limites inferior e superior da integral, respectivamente, para
a menor (d) e a maior (d + L) distˆancia entre um elemento infinitesimal da
barra e a part´ıcula, temos:
|
#”
F
res
| =
G · m
1
· M
L
Z
d+L
d
1
r
2
dr (6)
|
#”
F
res
| =
G · m
1
· M
L
·
(−1)
r
d+L
d
=
G · m
1
· M
L
·
(−1)
d + L
+
1
d
|
#”
F
res
| =
G · m
1
· M
L
·
(−d + d + L)
d · (d + L)
|
#”
F
res
| =
G · m
1
· M
d · (d + L)
(7)
Substituindo os valores fornecidos no enunciado, sendo G = 6, 67 ·
10
−11
m
3
kg·s
2
e tomando o devido cuidado para converter todas as unidades
para o Sistema Internacional (SI), obtemos |
#”
F
res
| = 3 · 10
−10
N
■
4
Livro - Fundamentos de f´ısica, volume 2, 8ª edi¸c˜ao, Halliday -
Resnick
Cap´ıtulo - 13, problema 21: Um planeta ´e modelado por um n´ucleo
de raio R e massa M cercado por uma casca de raio interno R, raio externo
2R e massa 4M. Se M = 4, 1 · 10
24
kg e R = 6, 0 · 10
6
m, qual ´e a acelera¸c˜ao
gravitacional de uma part´ıcula em pontos situados a uma distˆancia (a) R
e (b) 3R do centro do planeta?
Solu¸c˜ao:
Sabemos que o m´odulo da acelera¸c˜ao gravitacional a
g
´e dado por:
a
g
=
G · M
r
2
(1)
Para uma part´ıcula situada a uma distˆancia R do centro do planeta, a
equa¸c˜ao 1 pode ser reescrita como:
a
g
=
G · M
n´ucleo
R
2
(2)
Devemos recordar o teorema das cascas esf´ericas de Newton, segundo o
qual a for¸ca gravitacional resultante sobre uma part´ıcula no interior de uma
casca esf´erica ´e nula. Portanto, consideramos apenas a massa do n´ucleo do
planeta. Isso resulta:
a
g
=
6, 67 · 10
−11
· 4, 1 · 10
24
(6, 0 · 10
6
)
2
⇒ a
g
= 7, 60 m/s
2
Para uma part´ıcula localizada a uma distˆancia 3R do centro do planeta,
conforme o enunciado, ela est´a no exterior do planeta. Assim, devemos
considerar tanto a massa do n´ucleo quanto a massa da casca. Portanto,
reescrevemos a equa¸c˜ao 1 da seguinte maneira:
a
g
=
G · (M
n´ucleo
+ M
casca
)
(3R)
2
(3)
a
g
=
G · (M
n´ucleo
+ 4M
n´ucleo
)
(3R)
2
⇒ a
g
=
G · 5M
n´ucleo
9R
2
=
5
9
·
G · M
n´ucleo
R
2
a
g
=
5
9
· 7, 60 = 4, 22 m/s
2
■
5
Livro - Fundamentos de f´ısica, volume 2, 8ª edi¸c˜ao, Halliday -
Resnick
Cap´ıtulo - 13, problema 24: A Figura mostra duas cascas esf´ericas
concˆentricas homogˆeneas de massas M 1 e M 2 . Determine o m´odulo da
for¸ca gravitacional a que est´a sujeita uma part´ıcula de massa m situada a
uma distˆancia (a) a, (b) b e (c) c do centro comum das cascas.
Solu¸c˜ao:
Sabemos que o m´odulo da for¸ca gravitacional F
g
´e dado por:
F
g
=
G · M · m
r
2
(1)
Para uma part´ıcula situada a uma distˆancia a,no exterior de M
2
e no
exterior de M
1
, temos:
F
g
=
G · (M
1
+ M
2
) · m
a
2
Para uma part´ıcula localizada a uma distˆancia b, no interior de M
2
e
no exterior de M
1
, considerando o teorema das cascas esf´ericas de Newton,
temos:
F
g
=
G · M
1
· m
b
2
Para uma part´ıcula posicionada a uma distˆancia c, no interior de M
2
e
no interior de M
1
, considerando o teorema das cascas esf´ericas de Newton,
temos:
F
g
= 0
■
6
Livro - Fundamentos de f´ısica, volume 2, 8ª edi¸c˜ao, Halliday -
Resnick
Cap´ıtulo - 13, problema 36: Um proj´etil ´e lan¸cado verticalmente
para cima a partir da superf´ıcie da Terra. Despreze a rota¸c˜ao da Terra.
Em m´ultiplos do raio da Terra R
T
, que distˆancia o proj´etil atingir´a (a) se
a velocidade inicial for 0,500 da velocidade de escape da Terra e (b) se a
energia cin´etica inicial for 0,500 da energia cin´etica necess´aria para escapar
da Terra? (c) Qual ´e a menor energia mecˆanica inicial necess´aria para que
o proj´etil escape da Terra?
Solu¸c˜ao:
Considerando que, ao longo de toda a trajet´oria do proj´etil, sua energia
cin´etica K seja totalmente convertida em energia potencial gravitacional
U, ou seja, com a conserva¸c˜ao da energia mecˆanica E
m
, podemos escrever:
∆E
m
= E
final
− E
inicial
= [K + U]
final
− [K + U]
inicial
= 0 (1)
Sendo
K
final
= 0
U
final
= −
GMm
d
K
inicial
=
1
2
mv
2
i
U
inicial
= −
GMm
R
T
Escrevemos a equa¸c˜ao 1 da seguinte maneira:
−
GMm
d
= m
1
2
v
2
i
−
GM
R
T
−
GM
d
2
=
1
2
v
2
i
−
GM
R
T
(2)
Dessa forma, podemos aplicar as condi¸c˜oes iniciais do´ıtem (a) na euqa¸c˜ao
2, com v
i
=
1
2
v
e
, sendo v
e
=
q
2GM
R
T
, e, em seguida, determinar a distˆancia
d atingida pelo proj´etil. Vejamos:
−
GM
d
=
1
2
1
2
r
2GM
R
T
!
2
−
GM
R
T
(3)
−
GM
d
=
1
2
1
4
·
2GM
R
T
−
GM
R
T
7
−
GM
d
=
GM
4R
T
−
GM
R
T
=
GM
R
T
1
4
− 1
−
1
d
=
1
R
T
−
3
4
⇒
−
1
d
−1
=
−
3
4R
T
−1
d =
4
3
R
T
ou d = 1, 33R
T
Para o ´ıtem (b), aplicamos as condi¸c˜oes iniciais na equa¸c˜ao 1, com
K
inicial
=
1
2
1
2
mv
2
e
. Assim, obtemos:
−
GM
d
2
=
1
4
v
2
e
−
GM
R
T
(4)
−
GM
d
2
=
1
4
r
2GM
R
T
!
2
−
GM
R
T
=
GM
2R
T
−
GM
R
T
=
GM
R
T
1
2
− 1
−
1
d
=
1
R
T
−
1
2
⇒
−
1
d
−1
=
−
1
2R
T
−1
d = 2R
T
Para que o proj´etil escape da Terra, ´e necess´ario que ele alcance uma
distˆancia onde n˜ao esteja mais sob a influˆencia gravitacional do planeta.
Nesse ponto, tanto sua energia potencial quanto sua energia cin´etica s˜ao
nulas, pois toda a energia cin´etica foi completamente convertida em energia
potencial. Assim, a equa¸c˜ao 1 assume a seguinte forma:
∆E
m
= 0 ⇒ E
final
= E
inicial
= 0 (5)
Potanto, a energia mecˆanica inicial m´ınima necess´aria para o prj´etil es-
capar da terra ´e igual a zero.
■
8
Livro - Fundamentos de f´ısica, volume 2, 8ª edi¸c˜ao, Halliday -
Resnick
Cap´ıtulo - 13, problema 37: (a) Qual ´e a velocidade de escape de
um asteroide esf´erico com 500 km de raio se a acelera¸c˜ao gravitacional na
superf´ıcie ´e 3, 0 m/s
2
? (b) A que distˆancia da superf´ıcie chegar´a uma
part´ıcula se for lan¸cada da superf´ıcie do asteroide com uma velocidade
vertical de 1000 m/s ? (c) Com que velocidade um objeto se chocar´a
com o asteroide se for liberado sem velocidade inicial 1000 km acima da
superf´ıcie?
Solu¸c˜ao:
A condi¸c˜ao necess´aria para que um proj´etil de massa m escape da in-
fluˆencia gravitacional do asteroide ´e que ele alcance uma distˆancia em
rela¸c˜ao ao asteroide tal que, nesse ponto, tanto sua energia potencial grav-
itacional U quanto sua energia cin´etica K sejam nulas. Consequentemente,
a energia mecˆanica nesse ponto tamb´em ser´a nula. Assim, pela lei de con-
serva¸c˜ao da energia mecˆanica, a energia mecˆanica inicial, ou seja, com o
proj´etil na superf´ıcie, necess´aria para escapar do asteroide ´e zero. Pode-
mos, ent˜ao, escrever:
E
inicial
= K + U = 0 ⇒
1
2
mv
2
−
GMm
R
A
= 0 (1)
Com v = v
e
, velocidade de escape, R
A
e M, respectivamnte, o raio e a
massa do ateroide, escrevemos:
1
2
mv
2
e
=
GMm
R
A
⇒ v
e
=
r
2GM
R
A
(2)
Como o enunciado forneceu o m´odulo da acelera¸c˜ao gravitacional na su-
perf´ıcie, devemos colocar a velocidade de escape v
e
em termos da acelera¸c˜ao
gravitacional a
g
. Sendo a
g
=
GM
R
2
A
, n˜ao ´e dif´ıcil notar que se multiplicar-
mos o numerador e denominador da equa¸c˜ao 2 por R
A
conseguimos nosso
objetivo. Vejamos:
v
e
=
r
2GM
R
A
·
R
A
R
A
=
s
2GMR
A
R
2
A
=
p
2a
g
R
A
(3)
Substituindo os valores do enunciado e convertendo as unidades para o
sistema internacional (SI), obtemos v
e
= 1, 73 · 10
3
m/s.
9
Para determinar a distˆancia d da part´ıcula dado a condi¸c˜ao da veloci-
dade inicial v
i
= 10
3
m/s, podemos utilizar a lei da conserva¸c˜ao de energia
mecˆanica. Assim, podemos expressar;
E
final
= E
inicial
⇒ U(d) = K
inicial
+ U
inicial
(4)
−
GMm
d + R
A
=
1
2
mv
2
i
−
GMm
R
A
⇒ −
GM
d + R
A
=
1
2
v
2
i
−
GM
R
A
A partir deste ponto, todas as manipula¸c˜oes alg´ebricas buscam expressar
a distˆancia d de uma forma mais simples e econˆomica, em fun¸c˜ao das
informa¸c˜oes fornecidas. Outra forma de proseguir ´e encontrar o valor da
massa M atrav´es do m´odulo da acelera¸c˜ao gravitacional a
g
e, em seguida,
aplicar na equa¸c˜ao acima.
−
GM
d + R
A
·
R
2
A
R
2
A
=
1
2
v
2
i
−
GM
R
A
·
R
A
R
A
⇒ −
a
g
R
2
A
d + R
A
=
1
2
v
2
i
− a
g
R
A
−
a
g
R
2
A
d + R
A
−1
=
1
2
v
2
i
− a
g
R
A
−1
⇒ −
d + R
A
a
g
R
2
A
=
1
1
2
v
2
i
− a
g
R
A
d + R
A
=
−a
g
R
2
A
1
2
v
2
i
− a
g
R
A
⇒ d =
−a
g
R
2
A
1
2
v
2
i
− a
g
R
A
− R
A
Substituindo os valores do enunciado, obtemos d = 2, 5 · 10
5
m.
Ainda pela lei de conserva¸c˜ao da energia mecˆanica, temos na situa¸c˜ao
do ´ıtem (c) que toda a energia potencial gravitacional U, a uma distˆancia
h da superf´ıcie, deve ser convertida integralmente em energia cin´etica K.
Como o objeto parte do repouso sua energia cin´etica inicial ´e nula, sendo
assim, podemos escrever:
U
inicial
= [K + U]
final
⇒ −
GMm
h + R
A
=
1
2
mv
2
f
−
GMm
R
A
(5)
Com v
f
sendo a velocidade de chegada do objeto e h = 10
6
m. Isolando
v
f
, obtemos:
v
f
=
s
2
−
GM
(h + R
A
)
+
GM
R
A
=
s
2
−
GM
(h + R
A
)
·
R
2
A
R
2
A
+
GM
R
A
·
R
A
R
A
10
v
f
=
s
2
−
a
g
R
2
A
(h + R
A
)
+ a
g
R
A
=
s
−
2a
g
R
2
A
(h + R
A
)
+ 2a
g
R
A
Substituindo os valores encontramos v
f
= 1, 4 · 10
3
m/s.
■
11
Livro - Fundamentos de f´ısica, volume 2, 8ª edi¸c˜ao, Halliday -
Resnick
Cap´ıtulo - 13, problema 47: Um sat´elite ´e colocado em uma ´orbita
el´ıptica cujo ponto mais distante est´a a 360 km da superf´ıcie da Terra e cujo
ponto mais pr´oximo est´a a 180 km da superf´ıcie. Calcule (a) o semieixo
maior e (b) a excentricidade da ´orbita.
Solu¸c˜ao:
Sabemos, pela primeira Lei de Kepler, lei das ´orbitas, que um sat´elite em
´orbita el´ıptica ter´a a Terra localizada em um dos focos da elipse. Ent˜ao,
para resolver o ´ıtem (a) e encontrar o semi-eixo maior a, simplismente
podemos calcular a metade da soma das distˆancias do ponto mais distante
, o apogeu (D
A
) e do ponto mais pr´oximo, o perigeu (D
P
). Por´em, a Terra
n˜ao ´e um ponto, logo, devemos considerar suas dimens˜oes, incluindo o valor
do seu diˆametro (2R
T
) no c´alculo. Vejamos:
a =
D
A
+ D
P
+ 2R
T
2
(1)
Substituindo os valores do enunciado e sendo R
T
= 6, 37 · 10
6
m, obtemos
a = 6, 64 · 10
6
m.
Para o ´ıtem (b), podemos utilizar a defini¸c˜ao de excentricidade (e) de
uma elipse:
e =
c
a
(2)
Onde c ´e a disˆancia de um dos focos, centro da Terra, ao centro da elipse
e a ´e o semi-eixo maior.
Calcular c n˜ao ser´a dif´ıcil, pois a distˆancia do perigeu (D
P
) ´e fornecida.
Nesse caso, o semi-eixo maior a ser´a igual `a soma da distˆancia do perigeu
(D
P
), o raio da Terra (R
T
) e da distˆancia c. Vejamos:
a = D
P
+ R
T
+ c ⇒ c = a − D
P
− R
T
(3)
Substituindo o resultado acima na equa¸c˜ao 2, temos:
e =
a − D
P
− R
T
a
(4)
Substituindo os valores, obtemos e = 0,013 .
■
12
Livro - Fundamentos de f´ısica, volume 2, 8ª edi¸c˜ao, Halliday -
Resnick
Cap´ıtulo - 13, problema 49: (a) Que velocidade linear um sat´elite
da Terra deve ter para estar em ´orbita circular 160 km acima da superf´ıcie
da Terra? (b) Qual ´e o per´ıodo de revolu¸c˜ao?
Solu¸c˜ao:
Sabemos que existe uma rela¸c˜ao entre a energia potencial (U(d)) do
sat´elite em rela¸c˜ao a Terra e sua energia cin´etica (K) na ´orbita. Podemos
escrever:
K = −
U(d)
2
(1)
Seguindo as condi¸c˜oes do ´ıtem (a), ´orbita circular de raio d e h = 1, 6 ·
10
5
m, escrevemos:
1
2
mv
2
= −
(−GMm)
2d
⇒ v =
r
GM
h + R
T
(2)
Onde d = h+R
T
e M a massa da Terra. Substituindo os valores fornecidos
e sendo R
T
= 6, 37·10
6
m, M = 5, 98·10
24
kg, G = 6, 67·10
−11
m
3
kg·s
2
, obtemos
v = 7, 82 · 10
3
m/s.
Para encontrarmos o per´ıodo de revolu¸c˜ao, podemos uilizar a terceira
lei de Kepler, lei dos per´ıodos. Vejamos:
T
2
=
4π
2
GM
d
3
⇒ T =
s
4π
2
GM
(h + R
T
)
3
(3)
Substituindo os valores, obtemos T = 5, 25 · 10
3
s.
■
13
Livro - Fundamentos de f´ısica, volume 2, 8ª edi¸c˜ao, Halliday -
Resnick
Cap´ıtulo - 13, problema 62: Um sat´elite gira em torno de um planeta
de massa desconhecida em uma circunferˆencia com 2, 0 · 10
7
m de raio.
O m´odulo da for¸ca gravitacional exercida pelo planeta sobre o sat´elite ´e
F = 80 N. (a) Qual ´e a energia cin´etica do sat´elite? (b) Qual seria o
m´odulo F se o raio da ´orbita aumentasse para 3, 0 · 10
7
m?
Solu¸c˜ao:
A energia cin´etica (K) do sat´elite pode ser determinada utilizando a
equivalˆencia entre a for¸ca gravitacional (F
g
) e a for¸ca centr´ıpeta (F
c
) pela
segunda lei de Newton. Assim, podemos escrever:
F
g
= F
c
=
mv
2
r
(1)
F
g
·
r
2
=
mv
2
r
·
r
2
F
g
·
r
2
= K (2)
Substituindo os valores, obtemos K = 8, 0 · 10
8
J.
Sabemos que a for¸ca gravitacional F
g
´e inversamente proporcional ao
quadrado da distˆancia entre as massas. Dessa forma, podemos expressar:
F
g
=
C
r
2
⇒ C = F
g
· r
2
(3)
Onde C ´e uma constante. Ent˜ao, considerando a cen´ario inicial [F
g
·r
2
]
inicial
e cen´ario final [F
g
· r
2
]
final
, escrevemos:
[F
g
· r
2
]
inicial
= [F
g
· r
2
]
final
(4)
[F
g
· r
2
]
inicial
[r
2
]
final
= [F
g
]
final
Onde [F
g
· r
2
]
inicial
= 80 · (2, 0 · 10
7
)
2
e [r
2
]
final
= (3, 0 · 10
7
)
2
. Obtemos
[F
g
]
final
= 35, 55 N
■
14
Livro - Fundamentos de f´ısica, volume 2, 8ª edi¸c˜ao, Halliday -
Resnick
Cap´ıtulo - 13, problema 90: A maior velocidade de rota¸c˜ao poss´ıvel
de um planeta ´e aquela para a qual a for¸ca gravitacional no equador ´e
igual `a for¸ca centr´ıpeta. (Por quˆe?) (a) Mostre que o per´ıodo de rota¸c˜ao
correspondente ´e dado por
T =
r
3π
Gρ
em que ρ ´e a massa espec´ıfica do planeta esf´erico e homogˆeneo. (b) Calcule
o per´ıodo de rota¸c˜ao supondo uma massa espec´ıfica de 3, 0 g/cm
3
, t´ıpica
de muitos planetas, sat´elites e asteroides. Nunca foi observado um astro
com um per´ıodo de rota¸c˜ao menor que o determinado por essa an´alise.
Solu¸c˜ao:
Respondendo `a pergunta inicial, no caso de a velocidade de rota¸c˜ao ser
t˜ao alta que n˜ao haja equivalˆencia entre a for¸ca gravitacional e a for¸ca
centr´ıpeta, os objetos soltos no equador seriam arremessados. Isso ocorre
porque uma maior velocidade angular implica uma for¸ca centr´ıpeta maior
do que a for¸ca gravitacional.
Sabendo que vale a equivalˆencia entre a for¸ca gravitacional e a for¸ca
centripeta, podemos escrever:
F
g
= F
c
=
mv
2
R
(1)
da´ı,
GMm
R
2
=
mv
2
R
Onde M ´e a massa do planneta, m ´e a massa do corpo na superf´ıcie e R ´e
o raio do planeta. Assm, expressamos:
GM
R
= v
2
(2)
Nosso objetivo ´e mostrar a express˜ao dada para o per´ıodo de rota¸c˜ao, ent˜ao,
lembremos que
v = ω · R , ω =
2π
T
, M = ρ · V e V =
4
3
π · R
3
. Substituindo na equa¸c˜ao 2, obtemos:
15
G
R
·
ρ ·
4
3
πR
3
= (ω · R)
2
=
2π
T
2
· R
2
=
4π
2
T
2
· R
2
assim,
Gρ · 4πR
2
3
=
4π
2
R
2
T
2
ent˜ao,
Gρ
3
=
π
T
2
explicitando T :
T =
r
3π
Gρ
(3)
assim como quer´ıamos mostrar.
O item (b) pode ser resolvido apenas convertendo ρ = 3, 0 g/cm
3
para as
unidades padr˜ao do SI, o que resulta em ρ = 3, 0 · 10
3
kg/m
3
. Substituindo
na equa¸c˜ao 3, obtemos T = 6, 86 · 10
3
s
■
16
%20(1).png)

Comentários
Postar um comentário