Por que a correnteza acelera quando o rio se estreita? Conheça o Efeito Venturi.

 Por que a correnteza acelera quando o rio se estreita? Conheça o Efeito Venturi.

Neste post, vamos abordar uma consequência do princípio da conservação de energia aplicado ao escoamento de um fluido em regime estacionário, no qual as partículas do fluido seguem uma trajetória bem definida. Ao passar por uma 'garganta', uma região estreita, ocorrem variações na pressão e na velocidade. Este fenômeno, conhecido por Efeito Venturi, recebeu esse nome em homenagem ao engenheiro Giovanni Venturi, responsável pelo desenvolvimento do Medidor de Venturi. Podemos demonstrá-lo facilmente usando a equação de Bernoulli e a equação da continuidade. Além disso, aplicaremos esses conceitos para responder à pergunta do título.

Efeito Venturi, a Equação de Bernoulli e a Equação da Continuidade

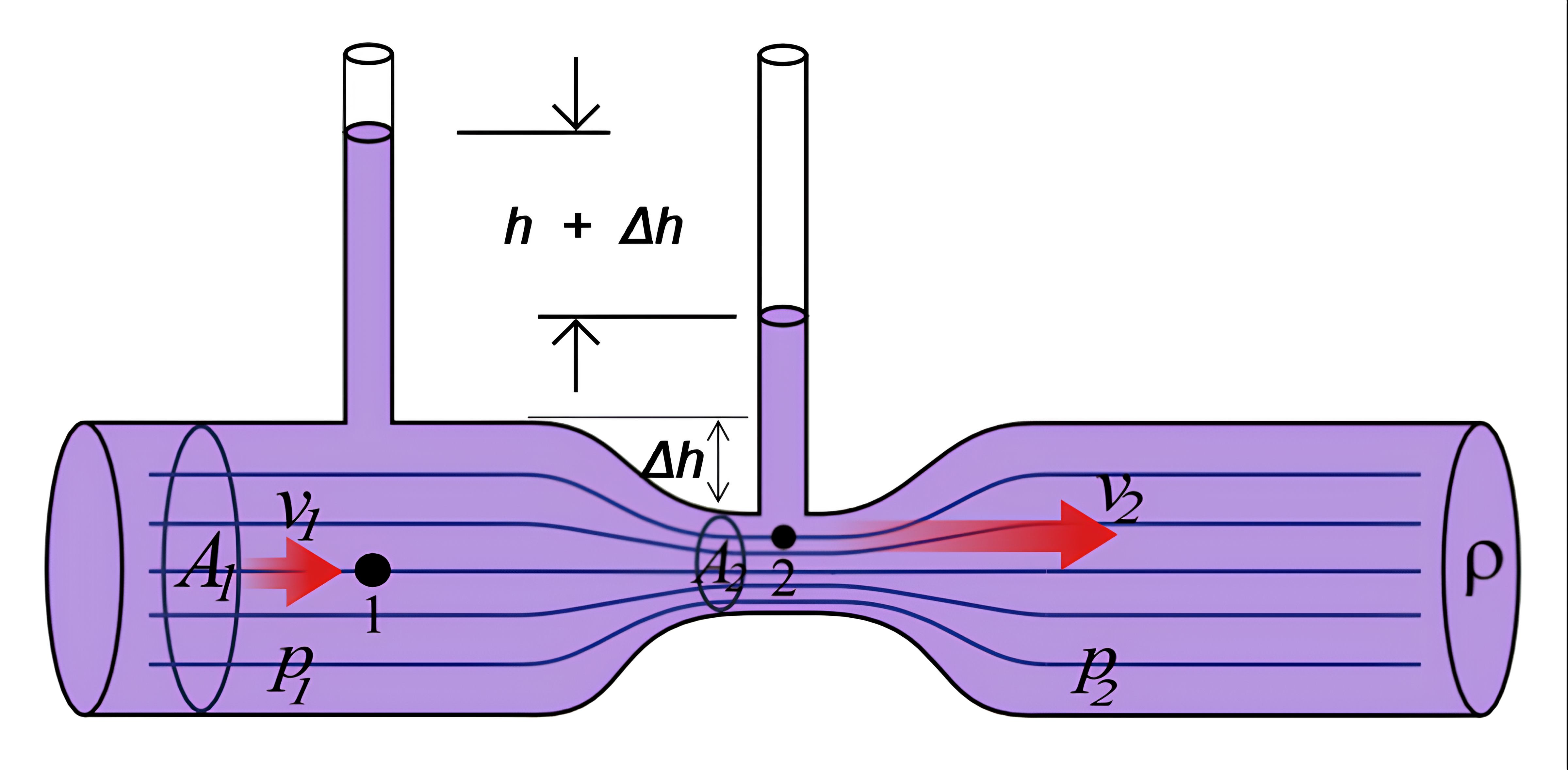Figura 1: Efeito Venturi. Disponível em: <https://pt.wikipedia.org/wiki/Efeito_Venturi>


Suponhamos o escoamento estacionário de um fluido incompressível, densidade constante, por um tubo horizontal de seção reta transversal variável. No ponto 1 e 2, respectivamente, o tubo possui uma secção de área $A_1$ e $A_2$. Veja o modelo apresentado na figura 1. No ponto 1, o fluido apresenta pressão $P_1$ e velocidade $v_1$, já no ponto 2, a pressão é $P_2$ e velocidade, $v_2$. Além disso, consideremos o deslocamento do fluido do ponto 1 ao ponto 2 completamente na horizontal, sem variação na altura, ou seja, $y_1 = y_2 $. Nessas condições, podemos expressar a equação de Bernoulli da seguinte forma: 

$$ P_1 + \frac{1}{2} \rho v_1^2 = P_2 + \frac{1}{2} \rho v_2^2$$

A equação da continuidade, baseada no princípio da conservação de massa, estabelece que a vazão se mantém constante ao longo do escoamento. A partir dessa equação, podemos determinar a relação entre a área da seção transversal e a velocidade de escoamento nos pontos 1 e 2. Vejamos: 

$$A_1 \cdot v_1 = A_2 \cdot v_2$$

então,

$$v_2 = \frac{A_1}{A_2} v_1$$

Essa última equação nos mostra que a velocidade no ponto 2, $v_2$, é maior que a velocidade no ponto 1, $v_1$,  pois a área $A_1$, é maior que a área $A_2$. Como consequência, para que a igualdade na equação de Bernoulli seja mantida, deve ocorrer uma variação na pressão. Para nos convencermos dessa variação, podemos substituir essa ultima equação na equação de Bernoulli. Ao analisar o sinal dessa variação, positivo ou negativo, podemos determinar se a pressão aumenta ou diminui. Vejamos: 

‌$$ P_1 + \frac{1}{2} \rho v_1^2 = P_2 + \frac{1}{2} \rho (\frac{A_1}{A_2} v_1)^2$$

isolando a variação $P_1 - P_2$,

$$ P_1 - P_2 = \left(\frac{A_1}{A_2}\right)^2 \frac{1}{2} \rho v_1^2 - \frac{1}{2} \rho v_1^2$$

simplificando,

$$ P_1 - P_2 = \left[ \left(\frac{A_1}{A_2}\right)^2 - 1 \right]\frac{1}{2} \rho v_1^2$$

É fácil perceber que o coeficiente $ \left[ \left(\frac{A_1}{A_2}\right)^2 - 1 \right]$ é um número positivo. Assim, para que $P_1 - P_2$ também seja positivo, é necessário que  $P_1$ seja maior que $P_2$. Dessa forma, fica demonstrado que, nas condições descritas inicialmente, a redução da área da seção transversal resulta em um aumento da velocidade de escoamento e uma diminuição na pressão.

Medidor de Venturi

Figura 2: Medidor de Venturi. Halliday; Resnick; Walker, Fundamentos de Física , vol. 2, 8ª edição, 2009, p. 83.

Uma aplicação direta do Efeito Venturi é o medidor de Venturi (ver Figura 2). Um medidor de Venturi é um instrumento utilizado para medir a velocidade de escoamento de um fluido ou a vazão em uma tubulação. O medidor é conectado entre dois segmentos do cano. A entrada e saída do medidor deve possuir a mesma seção transversal $A$ do cano. A velocidade de entrada $v_1$, que corresponde à mesma velocidade do fluido no cano, pode ser obtida pela equação que já encontramos, desde que saibamos a diferença de pressão, $P_1 - P_2$, entre a pressão no ponto 1 (no cano), e a pressão no ponto 2 (no estreitamento, seção transversal $a$). Para isso, o medidor é acompanhado por um manômetro, que registra a variação da pressão por meio da diferença de nível $h$ de um fluido de densidade $\rho_f$.

Resolvendo a equação de Bernoulli e a equação da continuidade em relação a velocidade $v_1$ para o caso da Figura 2, temos: 

$$ P_1 - P_2 = \left[ \left(\frac{A}{a}\right)^2 - 1 \right]\frac{1}{2} \rho v_1^2$$

isolando $v_1$,

$$ v_1 = \sqrt{\frac{2(P_1 - P_2)}{\rho \left[ \left( \frac{A}{a}\right)^2 - 1\right]}}$$

simplificando,

$$ v_1 = a\sqrt{\frac{2(P_1 - P_2)}{\rho \left[ A^2 - a^2\right]}}$$

No manômetro, pelo princípio de Stevin, temos: 

$$ P_1 - P_2 = \rho_f g h$$

Assim, 

$$ v_1 = a\sqrt{\frac{2(\rho_f g h)}{\rho \left[ A^2 - a^2\right]}}$$

Conseguimos uma expressão da velocidade no cano $v_1$ em termos de constantes bem definidas pelas condições iniciais.

Para o modelo do medidor de Venturi apresentado na Figura 1, a última equação sofre uma leve modificação. Como a diferença de pressão, $P_1 - P_2$, é medida por um manômetro que utiliza o próprio fluido da tubulação, temos que $\rho_f = \rho$. Logo, de acordo com as nomenclaturas definidas para a Figura 1, temos:

$$ v_1 = A_2\sqrt{\frac{2 g h}{A_1^2 - A_2^2}}$$

Física no cotidiano


Agora, retomemos à pergunta do título. Em um rio que apresenta um estreitamento das margens, como ilustrado na Figura 3, ocorre uma situação análoga ao Efeito Venturi. Devido a essa redução na largura, a velocidade da correnteza aumenta.

Outra aplicação interessante é a atração entre duas garrafas quando um fluxo de ar passa por uma pequena abertura entre elas, como mostrado na Figura 4. Esse fenômeno também está relacionado à variação de pressão prevista pelo Efeito Venturi.


Figura 4. Fenômeno de Venturi: atração. Disponível em: <https://www.youtube.com/watch?v=tT9k3lF5nEA>. 

‌

Devido à menor pressão entre as garrafas, a pressão do ar em volta exerce uma força que as empurra uma em direção à outra.

Além desses, o Efeito Venturi está presente em diversos outros casos do dia a dia. Você conseguiria identificar esses outros exemplos?

Bibliografia e sugestões de leitura

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física. 8ª ed. Rio De Janeiro: Ltc, 2009. v. 2

NUSSENZVEIGH. MOYSÉS. Curso de Física Básica : Fluidos, Oscilações e Ondas, Calor. São Paulo: Editora Edgard Blucher Ltda., 2018.


The Venturi effect. What it is and its application fields. Disponível em: <https://www.pericoli.com/en/the-venturi-effect-what-it-is-and-its-application-fields/>.

‌


‌






Comentários

Postar um comentário

Postagens mais visitadas deste blog

Tubo de Pitot e a Equação de Bernoulli: Como Medir a Velocidade de um Fluido?

Imagem
Tubo de Pitot e a Equação de Bernoulli: Como Medir a Velocidade de um Fluido? Você já se perguntou como um avião consegue medir sua velocidade no ar? Para isso, ele utiliza um dispositivo fundamental da mecânica dos fluidos: o tubo de Pitot . Esse instrumento, baseado na equação de Bernoulli , permite determinar a velocidade de um fluido a partir da diferença de pressão entre dois pontos. A equação de Bernoulli descreve a conservação de energia em um fluido em movimento e é muito aplicada em diversas áreas. No caso do tubo de Pitot, em determinadas condições, essa equação possibilita calcular com precisão a velocidade do ar ao redor de uma aeronave, por exemplo. Neste post, exploraremos como a equação de Bernoulli é aplicada no tubo de Pitot, explicando seu funcionamento e demonstrando sua importância com um exemplo prático. Sumário  A Equação de Bernoulli e o Princípio da Conservação de Energia  Aplicação da Equação de Bernoulli no Tubo de Pitot Física no cotidiano Bibliogra...
Leia mais

Momento de Inércia: Teorema dos eixos paralelos, Teorema dos eixos perpendiculares e Raio de giração.

Imagem
Momento de Inércia: Teorema dos eixos paralelos, Teorema dos eixos perpendiculares e Raio de giração. Neste post, exploraremos alguns resultados relevantes para o cálculo do momento de inércia de corpos rígidos. Inicialmente, demonstramos o teorema dos eixos paralelos , fundamental para determinar o momento de inércia quando o eixo de referência não passa pelo centro de massa do corpo.  Em seguida, apresentamos o teorema dos eixos perpendiculares , aplicável a corpos planos. Esse teorema permite calcular o momento de inércia em relação a um eixo perpendicular ao plano, utilizando os momentos de inércia já conhecidos em dois eixos de referência que se interceptam em ângulo de 90°.   Por fim, abordamos uma generalização interessante: é possível calcular o momento de inércia de qualquer corpo rígido em relação a um eixo arbitrário, substituindo-o por um aro de mesma massa e com u m raio equivalente à distância necessária para concentrar toda a massa do corpo de forma que seu...
Leia mais