Tubo de Pitot e a Equação de Bernoulli: Como Medir a Velocidade de um Fluido?
Tubo de Pitot e a Equação de Bernoulli: Como Medir a Velocidade de um Fluido?
Você já se perguntou como um avião consegue medir sua velocidade no ar? Para isso, ele utiliza um dispositivo fundamental da mecânica dos fluidos: o tubo de Pitot. Esse instrumento, baseado na equação de Bernoulli, permite determinar a velocidade de um fluido a partir da diferença de pressão entre dois pontos.
A equação de Bernoulli descreve a conservação de energia em um fluido em movimento e é muito aplicada em diversas áreas. No caso do tubo de Pitot, em determinadas condições, essa equação possibilita calcular com precisão a velocidade do ar ao redor de uma aeronave, por exemplo.
Neste post, exploraremos como a equação de Bernoulli é aplicada no tubo de Pitot, explicando seu funcionamento e demonstrando sua importância com um exemplo prático.
A Equação de Bernoulli e o Princípio da Conservação de Energia
A equação de Bernoulli é uma aplicação direta do princípio da conservação de energia para fluidos em escoamento laminar. Sua forma geral é:
Onde:
- $P = \text{Pressão}$.
- $\rho = \text{Densidade do fluido}$.
- $v = \text{Velocidade do fluido}$.
- $g = \text{Acelerção da gravidade}$.
- $y = \text{Altura}$.
Ela mostra que a soma da pressão, da energia cinética e da energia potencial por unidade de volume se mantém constante ao longo do fluxo, desde que não haja dissipação de energia.
Essa simplificação permite determinar a velocidade do fluido a partir da diferença de pressão entre dois pontos, a base do funcionamento do tubo de Pitot. Nos próximos tópicos, veremos como essa equação é aplicada na prática.
Aplicação da Equação de Bernoulli no Tubo de Pitot
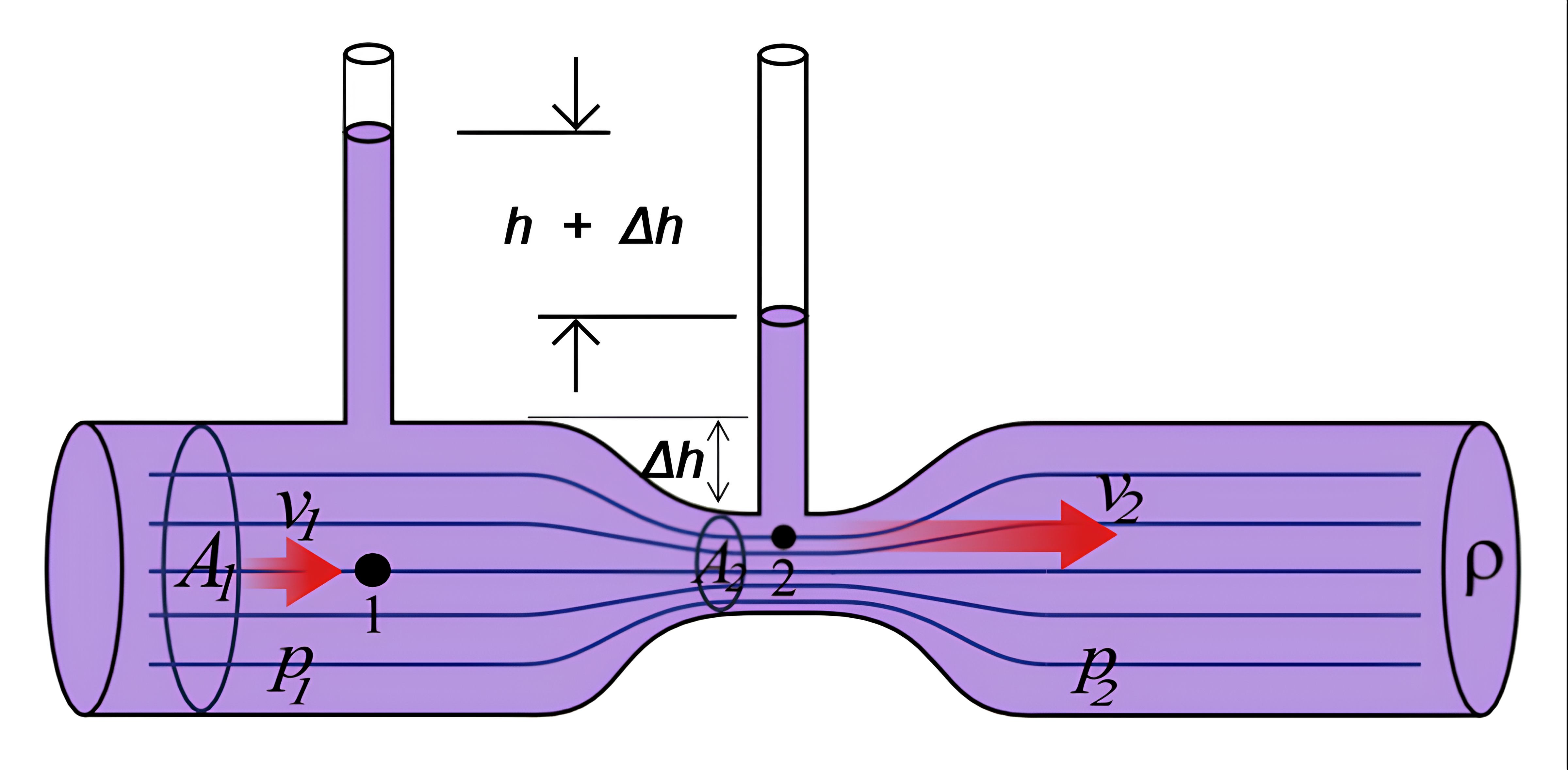
%20(1).png) |
| Figura 1: Tubo de Pitot. Halliday; Resnick; Walker, Fundamentos de Física , vol. 2, 8ª edição, 2009, p. 84. |
O tubo de Pitot foi criado por Henri Pitot em 1732 para medir a velocidade de fluxo de fluidos. Ele funciona como medidor de pressão diferencial, ou seja, mede duas pressões: a pressão estática ($P_e$) e a pressão total ($P_t$) (ou de estagnação). De uma maneira geral, um tubo de Pitot é formado por um compartimento onde é medido a pressão estática, outro para medida da pressão total com a abertura voltada diretamente para o fluxo e um equipamento conectado aos dois capaz de mostrar a diferença de pressão entre eles, permitindo a determinação da velocidade do fluxo.
A pressão estática ($P_e$) é a pressão do fluido em repouso ao redor do tubo, sendo medida perpendicularmente ao fluxo. Na figura 1, os furos marcados com a letra $\bf{B}$ permitem a entrada de ar, garantindo que a pressão dentro do tubo seja igual à pressão estática do ar externo.
Já a pressão total ($P_t$) é a soma da pressão estática e da pressão dinâmica ($P_d$). Ela é medida no ponto onde o fluxo atinge a abertura do tubo de Pitot, indicado na figura 1 pelo ponto $\bf{A}$. Para medir essa pressão de impacto, a maioria dos tubos de Pitot usa um tubo pequeno, frequentemente em forma de L. A partir da pressão dinâmica, que é a diferença entre a pressão total e a estática, é possível determinar a velocidade do fluxo. No modelo da figura 1, o tubo em formato de U com um líquido de densidade $\rho$ (manômetro) é responsável por medir a diferença entre a pressão estática e a pressão total.
Vejamos agora como a equação de Bernoulli pode ser aplicada para demonstrar o funcionamento do modelo de tubo de Pitot apresentado na figura 1.
Analisando um ponto qualquer fora do tubo de Pitot, e considerando que o fluido se move horizontalmente, ou seja, $\Delta y = 0$, e sabendo que no ponto de impacto, ponto A, a velocidade do fluxo é igual a zero, podemos expressar a equação de Bernoulli da seguinte forma:
$$P_t = P_e + \frac{1}{2}\rho_{ar} v^2$$.
Onde:
- $P_t \text{é a pressão no ponto} \bf{A}$.
- $P_e \text{ é a pressão estática do ar (pressão medida em}$ $\bf{B}$).
- $v \text{é a velocidade do ar}$.
Isolando a velocidade ($v$), obtemos:
No contexto da figura 1, podemos determinar a pressão dinâmica em função da diferença de nível ($h$) do líquido de densidade ($\rho$) no tubo com formato de U (Manômetro). Vejamos:
A conexão da esquerda do manômetro está ligada ao furo no ponto $\bf{A}$ com pressão total ($P_t$), já a conexão da direita está ligada ao compartimento com pressão estática $P_e$. Considerando isso e pelo princípio de Stevin, temos:
$$ P_t = P_e + \rho g h$$
Física no cotidiano
Suponha que o tubo apresentado na figura 1 contém álcool e que a diferença de nível $h$ é de $26,0$ $cm$. Qual é a velocidade do avião em relação ao ar? A massa específica do ar é $1,03$ $kg/m^3 $e a do álcool é $810$ $kg/m^3$. (Halliday; Resnick; Walker, 2009, p.84)
Para resolver o problema proposto, basta aplicar os valores fornecidos na equação da velocidade, lembrando de converter todas as unidades para o sistema internacional (SI). Vejamos:
$$ v = \sqrt{\frac{2 ( 810 \cdot 9,81 \cdot 2,6 \cdot 10^{-1} )}{1,03 }}$$
A equação de Bernoulli aplicada ao tubo de Pitot permitiu calcular que a velocidade do avião em relação ao ar é aproximadamente 228 km/h. Esse tipo de medição é essencial para o funcionamento dos instrumentos de navegação aérea, garantindo um voo eficiente e tranquilo.
Vimos que o tubo de Pitot é um exemplo prático da aplicação da equação de Bernoulli na medição da velocidade de um fluido. Sua importância é destacada em diversas áreas, como na aviação, onde é essencial para determinar a velocidade das aeronaves, além de ser utilizado em várias outras aplicações que envolvem o estudo e controle de fluxos de fluidos.
Bibliografia e sugestões de leitura
HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física. 8ª ed. Rio De Janeiro: Ltc, 2009. v. 2
AMBIENTAL, E. et al. Projeto de Física II Tubo de Pitot. [s.l: s.n.]. Disponível em: <https://www.sorocaba.unesp.br/Home/Extensao/Engenhocas/projeto-tubo-de-pitot.pdf>.
Agência Nacional de Aviação Civil. Disponível em: <https://www2.anac.gov.br/anacpedia/por_ing/tr1751.htm>.
BENSON, T. Pitot Tube. Disponível em: <https://www.grc.nasa.gov/WWW/k-12/VirtualAero/BottleRocket/airplane/pitot.html>.
Pitot Tube - Definition, Construction, Working, FAQs. Disponível em: <https://byjus.com/physics/pitot-tube/>.
VIEIRA, W. O que é e para que serve o tubo de Pitot? - WHL Engenharia. Disponível em: <https://whlengenharia.com.br/tubo-de-pitot/>.
Comentários
Postar um comentário