Momento de Inércia: Teorema dos eixos paralelos, Teorema dos eixos perpendiculares e Raio de giração.


Momento de Inércia: Teorema dos eixos paralelos, Teorema dos eixos perpendiculares e Raio de giração.

Neste post, exploraremos alguns resultados relevantes para o cálculo do momento de inércia de corpos rígidos. Inicialmente, demonstramos o teorema dos eixos paralelos, fundamental para determinar o momento de inércia quando o eixo de referência não passa pelo centro de massa do corpo. Em seguida, apresentamos o teorema dos eixos perpendiculares, aplicável a corpos planos. Esse teorema permite calcular o momento de inércia em relação a um eixo perpendicular ao plano, utilizando os momentos de inércia já conhecidos em dois eixos de referência que se interceptam em ângulo de 90°.  Por fim, abordamos uma generalização interessante: é possível calcular o momento de inércia de qualquer corpo rígido em relação a um eixo arbitrário, substituindo-o por um aro de mesma massa e com um raio equivalente à distância necessária para concentrar toda a massa do corpo de forma que seu momento de inércia seja preservado – o que definimos como raio de giração. Além disso, reformulamos os teoremas apresentados de modo a expressá-los em termos do raio de giração.

Teorema dos Eixos Paralelos





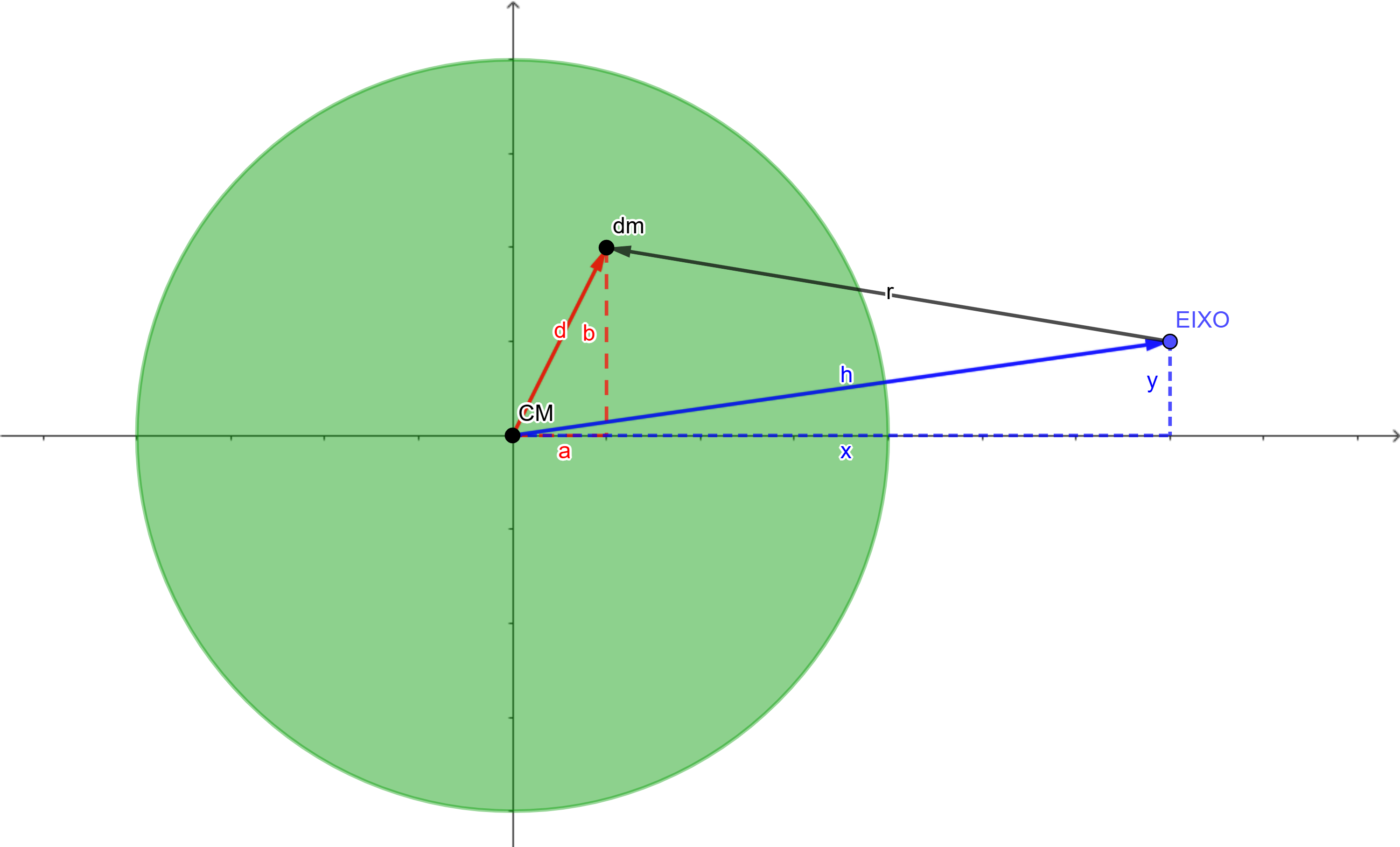
Na figura, é representado um corpo rígido genérico de massa total, $M$, cujo centro de massa ($CM$) está localizado na origem do sistema de coordenadas. Um elemento de massa, $dm$, está posicionado em relação ao centro de massa de acordo com o vetor $\bf{d}$ $ = (a,b)$, indicado em vermelho. Também é exibido a posição, em relação ao centro de massa, de um eixo de referência, que é perpendicular ao plano do corpo e paralelo ao eixo que passa pelo centro de massa, representada pelo vetor $\bf{h}$ $= (x,y)$ em azul. Por fim, o vetor $\bf{r}$, na cor preta, mostra a posição do elemento de massa $dm$ em relação a esse eixo de referência.

Nosso interesse é calcular o momento de inércia desse corpo rígido em relação ao eixo de referência. Para isso, precisamos calcular a contribuição infinitesimal, $dI$, para o momento de inércia de cada elemento de massa $dm$ localizado a um distância do eixo de referência, $r$, módulo do vetor $\bf{r}$. Assim, pela definição do momento de inércia, podemos escrever: 

$$dI = r^2 \cdot dm$$

Da geometria descrita na figura, podemos escrever o vetor $\bf{d}$, posição do $dm$ em relação ao $CM$, como uma soma entre os vetores $\bf{h}$ e $\bf{r}$.

$$\bf{d} = \bf{h} + \bf{r}$$

Daí,

$$\bf{r} = \bf{d} - \bf{h}$$

Assim, sabendo as componentes dos vetores $\bf{d}$ e $\bf{h}$ (veja a figura), conseguimos determinar as componentes do vetor $\bf{r}$. Vejamos:

$$\bf{r} = (a,b) - (x,y) $$

Logo,

$$\bf{r} = (a-x, b-y)$$

O módulo do vetor $\bf{r}$ é dado por:

$$r = \sqrt{(a-x)^2 + (b-y)^2}$$

Substituindo na primeira equação apresentada, temos:

$$dI = \left[ \sqrt{ (a-x)^2 + (b-y)^2 } \right]^2 \cdot dm $$

Simplificando e integrando ambos os membros da equação acima, escrevemos:

$$\int dI = \int   [(a-x)^2 + (b-y)^2]  \cdot dm $$

Daí,

$$ I = \int  [(a^2 - 2ax + x^2)+ (b^2-2by+y^2)] \cdot dm $$

Ajustando os termos dentro da integral de uma maneira conveniente, expressamos:

$$ I = \int  [(a^2 + b^2  - 2ax - 2by + x^2 +y^2)] \cdot dm $$

Assim,

$$ I = \int (a^2 + b^2) dm   -  \int 2ax dm - \int 2by dm + \int (x^2 +y^2) dm $$

Analisando termo a termo da equação acima, percebemos que:

$$ \int (a^2 + b^2) dm = \int d^2 dm = I_{CM}$$

Isto é, o momento de inércia do corpo em relação ao eixo que passa pelo seu centro de massa, $I_{CM}$;

$$ \int 2ax dm = 2aM \int \frac{x}{M}  dm = 0$$

É, pela definição, a coordenada x da localização do centro de massa de um corpo rígido. De forma análoga para a coordenada y, 

$$ \int 2ay dm = 2aM \int \frac{y}{M}  dm = 0$$

O centro de massa está localizado na origem do sistema de coordenadas, ponto $(0,0)$, então, o resultado das duas integrais acima é zero;

Por fim, o termo

$$ \int (x^2 +y^2) dm = \int h^2 dm$$

Sendo $h$ constante, podemos escrever

$$ \int h^2 dm = Mh^2$$

Portanto, o momento de inércia de um corpo rígido em relação a um eixo de referência paralelo e localizado a uma distância $h$ do eixo que passa pelo seu centro de massa é dado por:

$$I = I_{CM} + Mh^2$$

Teorema dos Eixos Perpendiculares



Na figura, é apresentado um corpo rígido plano com três eixos perpendiculares entre si, que se interceptam em um ponto comum, nesse caso, o centro de massa ($CM$) do corpo. Por conveniência, chamamos o eixo vermelho de $X$, o eixo amarelo de $Y$ e o eixo azul de $Z$. Também é ilustrado um elemento de massa, $dm$, do corpo rígido. As linhas tracejadas indicam as distâncias entre a posição do elemento de massa e os respectivos eixos. Para facilitar a compreensão, denominamos a distância representada em vermelho por $a$, a distância em amarelo por $b$ e a distância em azul por $c$.

Sem perda de generalidade, vamos calcular o momento de inércia do corpo em relação ao eixo $Z$. Sabemos que cada elemento de massa $dm$ contribui com um incremento $dI$ para o momento de inércia do corpo e, conforme definido acima, cada $dm$ está localizado a uma distância $c$ do eixo $Z$. Assim, podemos escrever:

$$dI = c^2 dm$$

Daí, integrando ambos os membros, obtemos:

$$I_Z = \int c^2 dm$$

Analisando a geometria da figura, é fácil perceber que a distância $c$ (linha tracejada em azul) está relacionada com as distâncias $a$ e $b$ -- representadas respectivamente, pela linha tracejada em vermelho e linha tracejada em amarelo -- por meio do teorema de Pitágoras. Ou seja, 

$$c^2 = a^2 + b^2$$

Unindo as duas últimas equações, podemos expressar:

$$I_Z = \int (a^2 + b^2) dm$$

Daí, 

$$I_Z = \int a^2 dm + \int b^2 dm$$

Onde

$$\int a^2 dm$$

é o momento de inércia do corpo em relação ao eixo $X$, $I_X$. De forma análoga,

$$\int b^2 dm$$

é o momento de inércia do corpo em relação ao  eixo $Y$, $I_Y$. Assim, podemos escrever:

$$I_Z = I_X + I_Y$$

Portanto, a expressão acima relaciona o momento de inércia de um corpo rígido plano em relação a um eixo perpendicular ao seu plano com os momentos de inércia medidos em relação aos eixos $X$ e $Y$ que se interceptam em um ponto.

Aro equivalente e Raio de Giração

Considere um corpo qualquer de massa $M$ com momento de inércia $I$ em relação a um eixo qualquer. Podemos substituir esse corpo por um aro de mesma massa $M$ e raio $K$ de tal forma que  o momento de inércia do aro, $I_{aro}$, seja igual ao momento de inércia desse corpo. Assim podemos, expressar:

$$I = I_{aro} = Mk^2$$

O valor de $k$ é definido como raio de giração. Do ponto de vista físico, o raio de giração representa a distância a partir do eixo de rotação na qual toda a massa do corpo poderia ser concentrada para resultar no mesmo momento de inércia. Da equação acima, determinamos uma expressão para $k$: 

$$k = \sqrt \frac{I}{M} $$

O raio de giração pode ser útil para facilitar a visualização da distribuição de massa de corpos complexos. De modo geral, um maior momento de inércia corresponde a um raio de giração maior, o que indica que a massa está distribuída mais  distante do eixo de referência.

Teorema dos Eixos Paralelos em Termos do Raio de Giração

Do teorema dos eixos paralelos, temos: 

$$ I = I_{CM} + Mh^2$$

Dividindo ambos os membros pela massa total $M$, obtemos: 

$$ \frac{I}{M} = \frac{I_{CM}}{M} + h^2$$

Da expressão do raio de giração e da ultima equação, podemos escrever: 

$$ k^2 = k_{CM}^2 + h^2$$

Essa equação mostra que o raio de giração $k$ em relação a um eixo qualquer é dado pelo raio de giração $k_{CM}$ em relação a um eixo que passa pelo centro de massa, acrescido da distância $h$ entre os dois eixos. Isto é, o deslocamento do eixo de referência em relação ao centro de massa contribui para o aumento do raio de giração do corpo.

Teorema dos Eixos Perpendiculares em Termos do Raio de Giração

Pelo teorema dos eixos perpendiculares, sabemos que

$$I_Z = I_X + I_Y$$

Dividindo ambos os membros pela massa total $M$, expressamos:

$$\frac{I_Z}{M}=\frac{I_X}{M} + \frac{I_Y}{M}$$

Assim, 
$$k_Z^2=k_X^2 + k_Y^2$$

Essa expressão mostra que o raio de giração em relação a um eixo perpendicular ao plano do corpo ($k_Z$) está relacionado aos raios de giração em relação aos eixos ortogonais contidos no plano do corpo ($k_X$ e $k_Y$).

Bibliografia 

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física. 8ª ed. Rio De Janeiro: Ltc, 2009. v. 1

NUSSENZVEIG, H. M. Curso de Física Básica. 1, Mecânica. São Paulo, Brasil: Blucher, 2018.




Comentários

Postar um comentário

Postagens mais visitadas deste blog

Tubo de Pitot e a Equação de Bernoulli: Como Medir a Velocidade de um Fluido?

Imagem
Tubo de Pitot e a Equação de Bernoulli: Como Medir a Velocidade de um Fluido? Você já se perguntou como um avião consegue medir sua velocidade no ar? Para isso, ele utiliza um dispositivo fundamental da mecânica dos fluidos: o tubo de Pitot . Esse instrumento, baseado na equação de Bernoulli , permite determinar a velocidade de um fluido a partir da diferença de pressão entre dois pontos. A equação de Bernoulli descreve a conservação de energia em um fluido em movimento e é muito aplicada em diversas áreas. No caso do tubo de Pitot, em determinadas condições, essa equação possibilita calcular com precisão a velocidade do ar ao redor de uma aeronave, por exemplo. Neste post, exploraremos como a equação de Bernoulli é aplicada no tubo de Pitot, explicando seu funcionamento e demonstrando sua importância com um exemplo prático. Sumário  A Equação de Bernoulli e o Princípio da Conservação de Energia  Aplicação da Equação de Bernoulli no Tubo de Pitot Física no cotidiano Bibliogra...
Leia mais

Por que a correnteza acelera quando o rio se estreita? Conheça o Efeito Venturi.

Imagem
  Por que a correnteza acelera quando o rio se estreita? Conheça o Efeito Venturi. Neste post, vamos abordar uma consequência do princípio da conservação de energia aplicado ao escoamento de um fluido em regime estacionário, no qual as partículas do fluido seguem uma trajetória bem definida. Ao passar por uma 'garganta', uma região estreita, ocorrem variações na pressão e na velocidade. Este fenômeno, conhecido por Efeito Venturi , recebeu esse nome em homenagem ao engenheiro Giovanni Venturi, responsável pelo desenvolvimento do Medidor   de Venturi. Podemos demonstrá-lo facilmente usando a equação de Bernoulli e a equação da continuidade . Além disso, aplicaremos esses conceitos para responder à pergunta do título. Sumário Efeito Venturi, a Equação de Bernoulli e a Equação da Continuidade Medidor de Venturi Física no cotidiano Bibliografia e sugestões de leitura Efeito Venturi, a Equação de Bernoulli e a Equação da Continuidade Figura 1: Efeito Venturi . Disponível em:...
Leia mais